一般 | 学生の方へ | 企業の方へ
分子や固体などの物質は電子と原子核から構成されています。 これらの系に対する支配方程式はDirac方程式として既に
知られています。 この方程式は1928年にDiracによって定式化されたものです。 もしDirac方程式を任意の系に
対して厳密に解くことが出来たならば、 原理的には実際の実験を行う前に物質の化学的・物理的性質を予言できるはずです。
これは物質科学における夢の一つです。 しかしながら簡単な系を除いてDirac方程式を厳密に解くことは
容易なことではありません。 なぜならば、数値的に厳密にこの方程式を解くための計算量がO(eN)として
増大することが知られているからです。ここでNは考えている系に含まれる
電子の数です。 現実的な観点から計算量と計算精度のバランスが取れた効率的な方法は密度汎関数理論です。この理論は
1964年にHohenbergとKohnによってその基礎付けが成されました。さらにこの理論に基き、1965年、実際的に計算を
実行する手法がKohnとShamによって提案され、現在ではKohn-Sham方程式として広く用いられるようになりました。
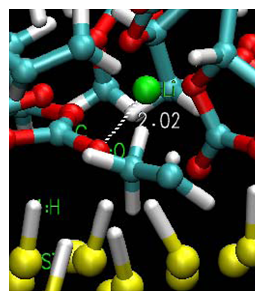我々の研究室では、密度汎関数理論に基く第一原理電子状態計算手法を数千原子から構成された大規模系に拡張するために、
効率的計算手法の開発に取り組んでいます。これまでにO(N)電子状態計算手法を含めた様々な低次スケーリング法の
開発に成功してきました。これらの新しい計算手法は第一原理電子状態計算プログラムパッケージ
OpenMX (Open source package for Material eXplorer)に組込まれ、GNU-GPLの規約に則り広く一般公開しています。
我々の開発したOpenMXは日本国内だけに留まらず、世界各国の研究機関でも応用研究に使用されるようになってきました。
これらの新しい計算手法と近年、急速に発展している超大規模並列計算機を用いて、応用上重要な挑戦的課題に取り組むことが
可能になりつつあります。第一原理計算の観点から複雑な物質のあるがままの姿を理解し、そして予測していくことが私達の
研究目標です。とりわけ以下に列挙する方法論・プログラムパッケージの開発に勢力的に取り組んでいます。
- 大規模密度汎関数計算のための効率的計算手法
- 準局所近似を越える電子状態計算手法
- 複雑な物質の取扱いを可能とする電子伝導計算手法
- 複雑なノンコリニア磁性(+スピン軌道相互作用)を取り扱うための計算手法
- OpenMX: GNU-GPLに基く第一原理電子状態計算プログラムパッケージ
- 超並列密度汎関数計算のための並列アルゴリズム
- シリセン: 新しいシリコン同素体
- ナノスケール導体の電気伝導計算
- 電気化学系の第一原理分子動力学計算
- 構造材料中の析出構造の第一原理電子状態計算
我々は計算物質科学と情報科学の境界領域の発展にも興味を持っています。与えられた物質の性質を予測するだけでなく、
望みの性質を持っている物質を設計することが最終的な目標となるでしょう。これは一つの逆問題であり、従来の計算物質科学
だけで解決する問題ではありません。
情報科学の分野で発展してきた様々な手法と計算物質科学を融合させる必要があるでしょう。
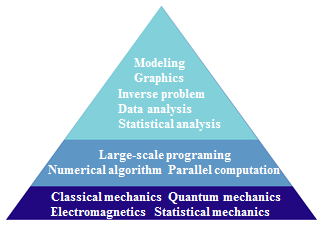この方向に向けても、研究を進めていきたいと考えています。
近い将来、計算物質科学が基礎研究だけでなく産業応用上の研究においても、ますます重要性が増してくると思われます。
今後の応用研究において、計算物質科学が『なくてはならないもの』として確立されるよう、私達は物理学、化学、数学、
情報科学、計算機科学を融合させることによって、計算物質科学のフロンティアを開拓していきたいと考えています。