General | To Students | To Companies
Materials such as molecules and bulks consist of electrons and nuclei, and the governing equation for the system
has been already known as i.e., the Dirac equation formulated by Dirac in 1928. If the equation were solved
exactly, chemical and physical properties of the system would be predicted before performing actual experiments
in principle, which is one of ultimate goals in materials science.
However, this is not possible except for very simple systems, since the computational cost for
solving the equation in a numerically exact sense may scale as O(eN), where N is
the number of electrons in a system.
An efficient way for practically solving the equation, balancing the computational accuracy and efficiency,
is the density functional theory (DFT) founded by Hohenberg and Kohn in 1964, and the Kohn-Sham equation developed
by Kohn and Sham in 1965.
We aim to develop DFT in a practical sense to extend applicability of the theory to large-scale realistic systems
including more than a few thousand atoms, and have succeeded to develop low-order scaling DFT methods including
O(N) methods, implemented in the OpenMX (Open source package for Material eXplorer) software package,
for the last ten years. With our continuous efforts we have been gradually able to address
challenging and industrially very important problems in accordance with recent remarkable
development of massively parallel computers, and reach better understanding of these complicated materials
from first-principle's point of view.
Especially, our research will cover the following methodological developments:
- Efficient methods and algorithms for large-scale DFT calculations
- Electronic structure methods beyond semi-local functionals
- Electronic transport methods enabling to address realistic systems
- Constraint non-collinear DFT methods with spin-orbit coupling
- OpenMX: GPL open source software package
- Parallel algorithms for massively parallel DFT calculations
- Silicenes: a new allotrope of Si
- Electronic transport problems of nano-scale conductors
- Electrochemical systems
We are also interested in an interdisciplinary area briding computational science and
information science to address an inverse problem on material design, while our activity
towards the direction is still on the drawing board.
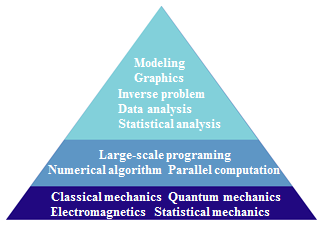
We are convinced that the computer-aided materials science will become
more and more important for not only fundamental researches, but also industrial researches in the near future.
We devote our efforts to extend frontiers of the computer-aided materials science by integrating a wide variety of
research areas including physics, chemistry, mathematics, and computer science so that the first-principle computer
simulations can be established as an invaluable tool for further development of materials science.