
Research Highlights:
O(N) exchange functional by a range-separated exchange hole
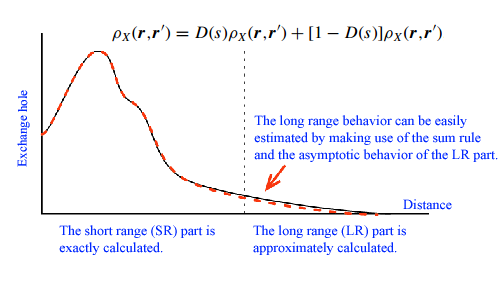
Widely used functionals such as local density approximations (LDA) and generalized gradient approximations (GGA) tend to fail to accurately predict band gap of insulators and semi-conductors, and grand state electronic structures of strongly correlated systems. A considerable part of the failure can be attributed to the self-interaction error (SIC) in these semi-local functionals. To overcome the difficulty and develop a nearly exact but computationally tractable exchange functional, we propose an approximation to the exchange-hole density for the evaluation of the exact exchange energy in electronic structure calculations within the density-functional theory (DFT) and the Kohn-Sham (KS) scheme. Based on the localized nature of density matrix, the exchange hole is divided into the short-range (SR) and long-range (LR) parts by using an adequate filter function, where the LR part is deduced by matching of moments with the exactly calculated SR counterpart, ensuring the correct asymptotic −1/ r behavior of the exchange potential. With this division, the time-consuming integration is truncated at a certain interaction range, largely reducing the computation cost to O(N). The total energies, exchange energies, exchange potentials, and eigenvalues of the highest occupied orbitals are calculated for the noble-gas atoms. The close agreement of the results with the exact values suggests the validity of the approximation.
