
Research Highlights:
交換ホールの実空間分割によるO(N)交換汎関数
密度汎関数理論において一般的に用いられる局所密度近似(LDA)や一般化勾配近似(GGA)は絶縁体や半導体の バンドギャップを推定する上で、十分な精度を持っていないことが知られています。また強相関系と呼ばれる局在d電子 (f電子)を持った系に対しても、基底状態の予測能は十分ではありません。
これらの凖局所密度汎関数における 問題の大部分は近似の際に導入された偽の自己相互作用に起因しています。電子が自分自身と相互作用すること で占有軌道のエネルギー準位が不安定化し、バンドギャップが小さくなります。また電子が自分自身と 相互作用してしまうと、クーロン反発を減少させるため、縮退軌道への電子占有は一様になる傾向があります。 軌道分極効果は同一軌道内の占有数を0もしくは1とすることで、クーロン反発を減少させる状態ですが、 自己相互作用を含んだ凖局所密度汎関数ではこの軌道分極効果の正しい記述は困難です。 自己相互作用を補正する方法の一つは、軌道に依存した厳密交換汎関数を用いることです。 自己相互作用の大部分は交換項から生じるため、厳密交換汎関数を用いることで、かなりの改善が 期待されます。しかし大規模系に対する厳密交換汎関数の計算は実際上は容易ではありません。
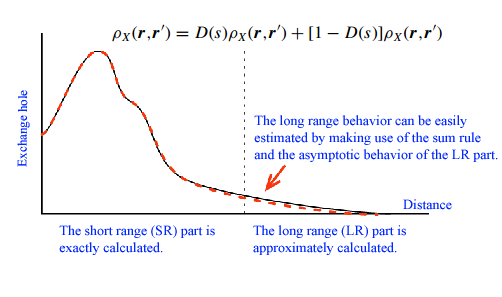
そこで私達は厳密交換汎関数の精度をできるだけ保持しながらも計算コストがO(N)となる新しい 交換汎汎関数の開発に取り組みました[1]。交換ホールは負定値条件を持ち、かつその空間積分値は -1となることが数学的に分かっています。また有限ギャップ系では交換ホールは実空間において 指数関数的に減衰することも知られています。この事実に基づき、我々は交換ホールを実空間で 分割し、(i) 近距離での交換ホールの微細構造を厳密に計算し、(ii) 遠距離での交換ホールの漸近形を 再現するようにモデル交換ホールを構築する、新しい交換汎関数法を提案しました。 計算コストはO(N)であり、大規模系への適用も可能だと考えています。 希ガス原子に対する計算は、本手法が交換エネルギー、交換ポテンシャル、最高被占有軌道の 固有値を高精度に計算できることを示しています。今後、我々はこの交換汎関数を利用して新しい 電子状態計算手法を開発していきたいと考えています。
