Ozaki Laboratory of ISSP

Research Highlights:

Numerically exact low-order scaling method

Figures (a)-(c) Nested dissection of a sparse matrix,
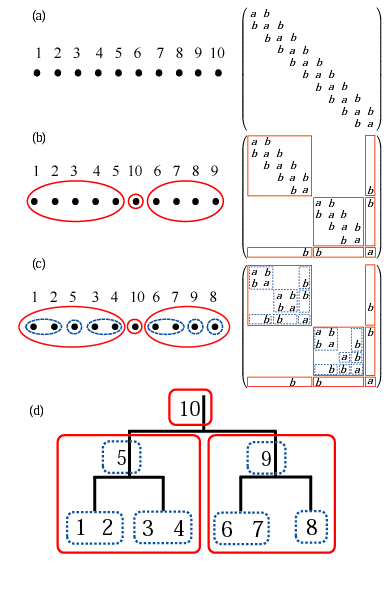
(d) binary tree structure showing interactions in the matrix (c).

Many scientific problems can be cast to an eigenvalue problem, and it is known that the computational cost of solving the eigenvalue problem scales as O(N³), where N is the dimension of the problem. The density functional theory (DFT) for molecules and solids is also cast to an eigenvalue problem within semi-local approximations such as local density and generalized gradient approximations, and thereby the computational cost must be O(N³). Thus, it is interesting to question whether the computational cost of the DFT calculation can be reduced from O(N³) to a low-order scaling or not without introducing approximations. We have addressed the problem and found that such a method can be actually developed by utilizing of locality of basis functions [1]. Our method directly computes selected elements of the density matrix by a contour integration of Green's function [2], which allows us to evaluate only O(N) density matrix elements due to the locality of basis functions. The Green's function is evaluated with a nested dissection approach for sparse matrices as shown in figure. It turns out that the computational effort of the method scales as O(N(log₂N)²), O(N²), O(N^7/3) for one-, two-, and three-dimensional systems, respectively. Unlike O(N) methods developed so far the approach is a numerically exact alternative to conventional O(N³) diagonalization schemes in spite of the low-order scaling, and can be applicable to not only insulating but also metallic systems in a single framework. It is also noted that the well separated data structure is suitable for the massively parallel computation. We expect that the direction will be furthermore explored in the near future to extend the applicability of DFT calculations for large-scale systems without sacrificing the accuracy.