
Research Highlights:
数値的に厳密な低次スケーリング対角化法
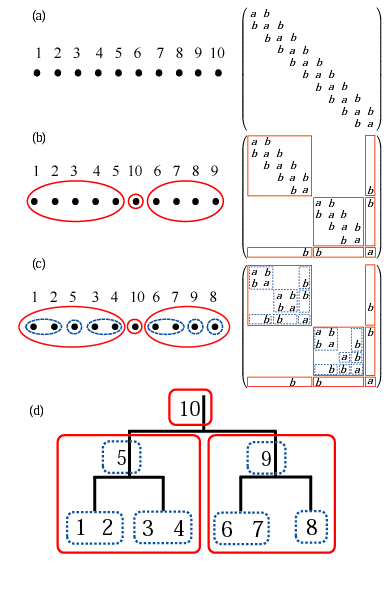
(d) 行列(c)の相互作用に対応する二分木構造
科学技術計算における問題の多くは固有値問題に帰着され、その計算コストは問題サイズNに対して O(N3)として増大することが知られています。分子や固体の電子状態を計算するための 密度汎関数理論もまた凖局所密度近似の範疇では、最終的に固有値問題に帰着され、したがってその 計算コストはO(N3)となります。固有値問題を解く際に近似の導入が許されるならば、 その計算コストはO(N)となることが知られていますが、近似を導入することなしに、その計算コストが 低次スケーリングとなる「数値的に厳密な低次スケーリング対角化法」は存在しないのでしょうか。
私達は近似を導入することなしに計算コストを削減できる新しい低次スケーリング法の開発に取り組みました[1]。 そして基底関数が局在している場合に、その様な計算手法が構築出来ることを見出しました。 私達の手法は二つにアイデアに基いています。一つ目のアイデアは密度行列の必要な成分のみを、 グリーン関数の留数積分から直接求めるというものです[2]。局在基底関数に対しては、計算に必要な 密度行列成分の個数はO(N)となります。また留数積分に必要なポール数が系のサイズに依存していない ことを数学的に証明できます。したがって全体の計算コストはグリーン関数の計算に支配されています。 二つ目のアイデアはグリーン関数の計算手法に関するものです。 私達は入れ子切断(nested dissection)法により疎行列を階層構造化させ(図を参照のこと)、 さらにLDLt分解をその階層構造化行列に対して再帰的に適用することで、 グリーン関数の必要な成分のみを求める漸化式を導出しました。漸化式に基づくグリーン関数の 計算コストは1次元、2次元、3次元系に対してそれぞれ、O(N(log2N)2), O(N2), O(N7/3)となり、近似を導入することなしに計算スケーリングの 低減が実現されました。本手法は絶縁体だけでなく、金属に対しても同様に適用可能で、また並列計算に 適したアルゴリズム構造を持っています。将来的には小規模系に対してはO(N3)法、 中規模系に対しては本手法、大規模系に対してはO(N)法と、目的に応じて固有値ソルバーを適切に 使い分けていくことを考えています。
