
Research Highlights:
第一原理電気伝導計算
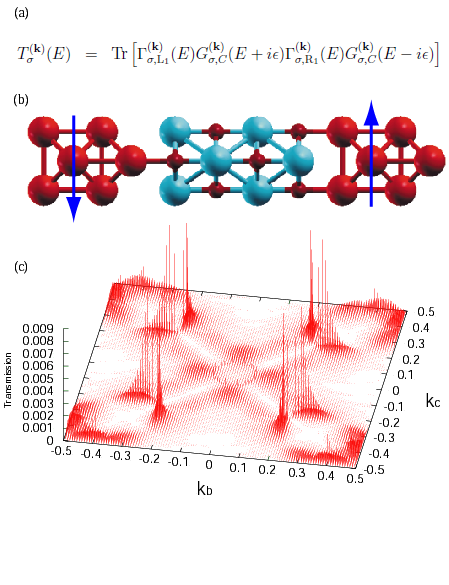
(c) 構造(b)のMgO層に対するk分解透過率スペクトル
近年の電子デバイス極小化の進展に伴い、実験と理論の溝は徐々に狭まりつつあります。 これらのナノスケール電子デバイスの電気伝導現象を定量的に取り扱うために、 最も信頼性の高い計算手法は非平衡グリーン関数(NEGF)法です。 さらにNEGF法を密度汎関数理論と組み合せることで、一般性の高い計算手法を 構築することが可能となります。この手法の特徴として、 (i) 同一の理論的枠組みで電極と散乱領域を取り扱うことが出来る、 (ii) 有限バイアス電圧下で散乱領域の電子状態を自己無撞着に計算できる、 (iii) フォノン散乱や電子間クーロン相互作用などの多体効果が自己エネルギーを通してほぼ同一の枠組みで取り込まれ得る、 (iv) 基底関数の局在性に基づいた定式化のため大規模系への適用が可能である、 などが挙げられます。
私達は最近、NEGF法の大規模系への適用性を拡張するために効率的な実装方法を開発し[1]、OpenMXへの 実装を行いました。NEGF法ではグリーン関数の積分によって密度行列を算出する部分が計算律速となりますが、 この積分を高精度かつ効率的に行うために、我々はフェルミ分布関数を連分数展開し、そのポールでの留数を 足し合わせる新しい方法を開発しました[2]。また二次元FFTと有限差分法を用いて電極-散乱領域間の境界条件付で ハートリーポテンシャルを容易に計算する新しい方法(FFT2D法)を開発しました。FFT2D法では境界条件を厳密に 再現することが可能であり、計算コストが小さくかつ並列性に優れるという利点を持っています。 私達は本実装の適用性を例証するため、ジグザググラフェンナノリボン、Fe/MgO/Feトンネル接合、 LaMnO3/SrMnO3超格子への応用計算を行い、本計算手法の有用性を 示しました。
本研究は産業技術総合研究所と物質・材料研究機構との共同研究として実施されました。
