
Research Highlights:
Absolute Binding Energies of Core Levels in Solids from First Principles

induced by the creation of a core hole
in the 2p states, where the unit cell
contains 1000 atoms and the intercore
hole distance is 27.15 Å.
Core levels excitation spectra by x-ray such as x-ray photoemission spectroscopy (XPS) and x-ray absorption near edge structure (XANES) have been widely used to prove chemical species, and geometrical, electronic, and magnetic structures in materials, especially surface region. In spite of the long history of XPS and its importance in materials science, a general and practical method had not been developed to calculate the absolute binding energies for both insulators and metals, including multiple splittings due to chemical shift, spin-orbit coupling, and exchange interaction, on equal footing. To qualitatively and quantitatively predict the spectra of complicated materials, we developed first-principles methods to calculate absolute binding energies of core levels in solids, which can be directly compared to XPS measurements, and x-ray absorption spectra. We first proved that the first excited state with a core hole can be rigorously calculated by density functional theories (DFT) in principle using the Gunnarsson-Lundqvist theorem. The proof implies that DFT provides an accurate framework to calculate the binding energies measured in XPS, since the XPS requires only the lowest excited state with (N-1) electrons. On the other hand, for the other spectroscopies including XANES and x-ray magnetic circular dichroism (XMCD), the lowest excitation must be calculated accurately by DFT, but higher excited states will be treated approximately. Based on the theorem, we developed a new method to calculate absolute binding energy of core level electrons in solid (metal, semiconductor, and insulator) with high accuracy based a penalty functional and exact Coulomb cutoff method [1]. The variational penalty functional enables us to treat multiple splittings due to chemical shift, spin-orbit coupling, and exchange interaction on equal footing, both of which are not accessible by previous methods, while the spurious interaction of core holes between supercells is avoided by the exact Coulomb cutoff method. As well as the ground state calculation, we calculate the total energy of the first excited state with a core hole on a targeted atom. The theorem allows us to perform the excited state calculation as a ground state calculation with a constraint which introduces the core hole.
 As shown in Table I, it is demonstrated that the absolute binding energies of core levels for both metals and insulators are calculated by the proposed method in a mean absolute (relative) error of 0.4 eV (0.16%) for eight cases compared to experimental values measured with x-ray photoemission spectroscopy within a generalized gradient approximation to the exchange-correlation functional. This is the first demonstration of such accurate calculations of absolute values for bulks by DFT. Since the excited state with the core hole is determined self-consistently, the many body effect is naturally taken into account. After the creation of core hole, other electrons try to screen the core hole potential as shown in Fig. 1. We see that the core hole is fully compensated by screening electron on the same atom with the core hole, and an oscillating behavior of charge density difference is observed as a result of the screening process.
As shown in Table I, it is demonstrated that the absolute binding energies of core levels for both metals and insulators are calculated by the proposed method in a mean absolute (relative) error of 0.4 eV (0.16%) for eight cases compared to experimental values measured with x-ray photoemission spectroscopy within a generalized gradient approximation to the exchange-correlation functional. This is the first demonstration of such accurate calculations of absolute values for bulks by DFT. Since the excited state with the core hole is determined self-consistently, the many body effect is naturally taken into account. After the creation of core hole, other electrons try to screen the core hole potential as shown in Fig. 1. We see that the core hole is fully compensated by screening electron on the same atom with the core hole, and an oscillating behavior of charge density difference is observed as a result of the screening process.

(b) by experiment, for (c) bucked structure by DFT,
(d) planar-like structure by DFT.
The second example is a collaboration with the Gohara group in the Hokkaido Univ. and the Yoshinobu group in ISSP to characterize the atomic and electronic structures of single atom dispersion of Pt on graphene [3]. In recent years, single atom dispersion of Pt atoms attracts much attention, since there might be a possibility that the amount of Pt can be reduced in use of the reduction catalysis. In collaboration with the Gohara group, we identified the detailed geometrical and electronic structures. It has been known that the binding energy (73ア0.4 eV) of Pt-4f7/2 core level of the single atom dispersion system is relatively higher than that (71.1 eV) of fcc Pt, and it was claimed that the high binding energy can be attributed to the oxidization of Pt atom. Our calculations show that the binding energy is close to 73 eV (Fig. 3(b)) if the Pt atom is bonded by three carbon atoms as shown in Fig. 3(a).
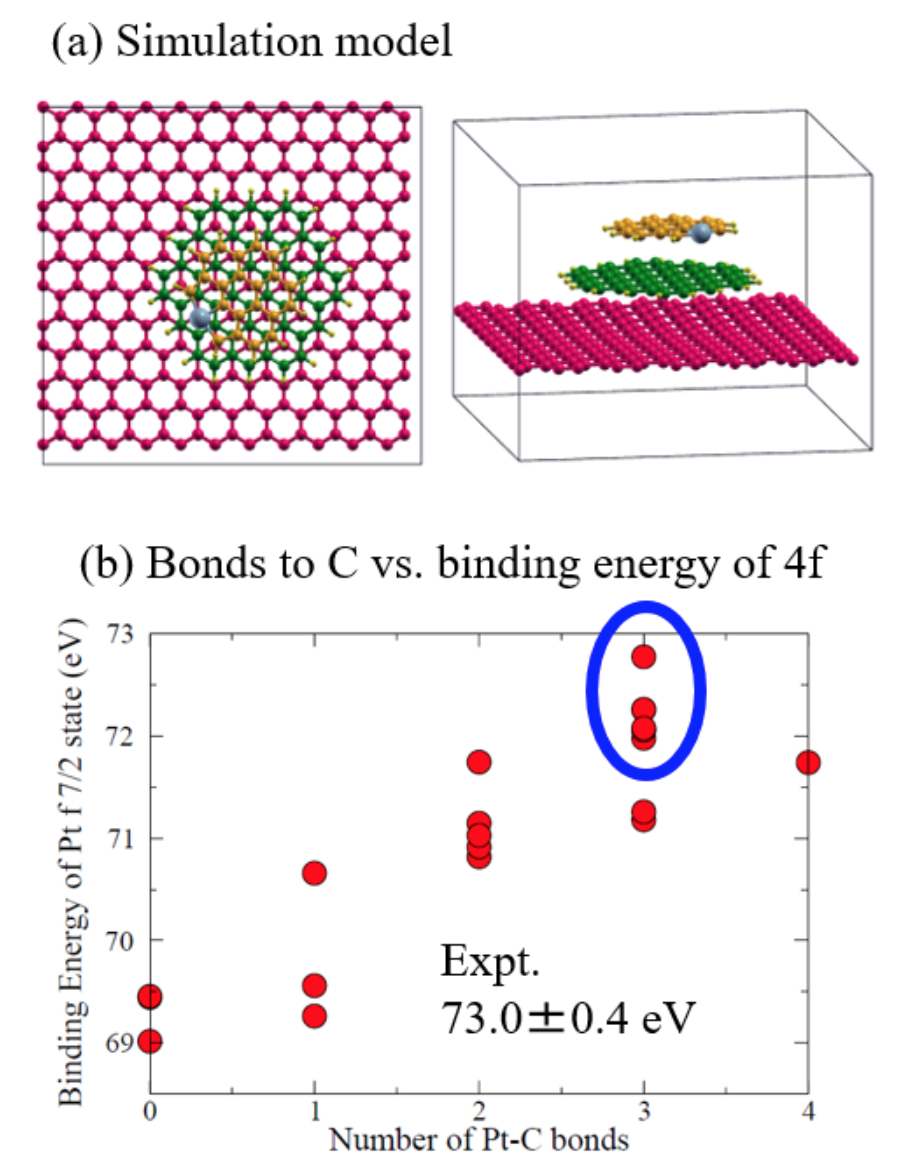
atom dispersion of Pt atoms
on graphene flake, (b) calculated
binding energy of Pt-4f7/2 as a
function of the number of Pt-C bonds.
From the analysis of electronic structure of Pt atom, it was found that the Pt 5dxy-orbital in the step edge plays a crucial role in the formation of chemical bonds to C atoms and in the considerable charge transfer from Pt to C atoms, resulting in the large binding energy shift of the Pt 4f state. By considering the good agreement of the binding energy and that the atomic structure is consistent to the HRTEM image, we concluded that Pt atoms are atomically dispersive on the graphene flake. This is the first identification of the single atom dispersion of Pt atoms. Furthermore, we have recently developed a first-principle method to calculate XANES spectra. It is also shown that the first excited state with a core hole is rigorously treated by DFT, while the exchange-correlation function has to be approximated, and the higher excited states are approximately evaluated on top of the first excited state. Along the same line, further extensions of the method can be possible for XMCD and electron energy loss spectroscopy (EELS), which may lead to a further extension of DFT.
