
Research Highlights:
Massive parallelization method for O(N) DFT calculations
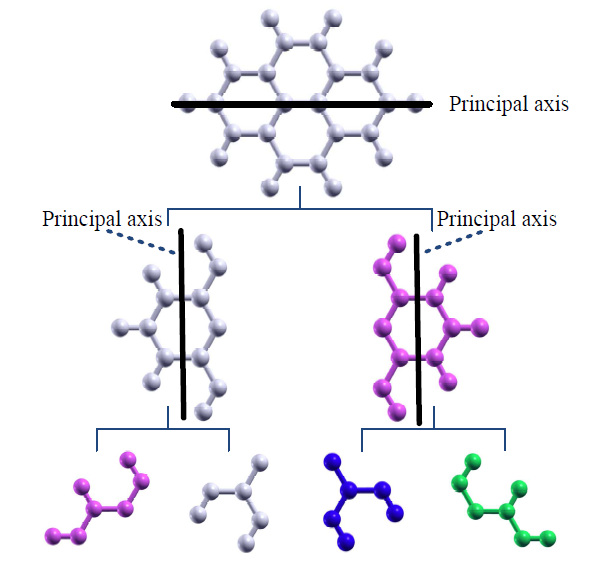
O(N) DFT methods, whose computational cost scales linearly as a function of the number of atoms, is one of effective ways to extend applicability of first-principles electronic structure calculations based on density functional theories (DFT) to large-scale systems including more than a dozen of thousand atoms. We have developed an O(N) method based on Krylov subspace so far, and demonstrated that the O(N) method can be applied to not only insulators but also metals. In the O(N) Krylov subspace method the system is decomposed to a set of small clusters, each of which has large overlap with the others, and each small cluster is solved in a Krylov subspace representation. After solving all the small cluster problem, the Green's functions associated with the central atom are collected to calculate charge density in the whole system. Thus, one can regard the method as one of divide and conquer methods. The algorithm is intrinsically suitable for the parallel calculation because of the independency of the cluster problems. However, it may not be obvious how the total system with an arbitrary dimensionality should be decomposed in space so that the computational memory and communication amount can be minimized for a given number of message passing interface (MPI) processes. To increase the parallel efficiency in the MPI parallelization, it is important to make data stored in each MPI process localized in space to minimize communication amount among the MPI processes. In addition, the computational load should be equilibrated over MPI processes to decrease an idling time. We have addressed the issue, and developed a new method of domain decomposition based on a modified recursive bisection method and an inertia tensor defined by the computational elapsed time [1].
The domain decomposition method consists of the following three steps: (1) For a given number of MPI processes a binary tree is constructed by a modified recursive bisection method. (2) A principle axis for a set of atoms is calculated by diagonalizing an inertia tensor matrix, and the atoms are projected onto the principle axis. (3) By employing the binary tree constructed by the step (1), the atoms are decomposed on the principle axis to two groups. As illustrated in Fig. 1, one can perform the domain decomposition of atoms by recursively performing the steps 2 and 3 with the binary tree constructed by the step 1, while keeping the locality of domain decomposition. In addition, it is possible to dynamically load balance among the MPI processes by making full use of the computational elapsed time for each atom at the previous step in geometry optimization and molecular dynamics simulations during the calculation of the inertia tensor. As an illustration, a result of the domain decomposition for diamond lattice is shown in Fig. 1, where the unit cell includes 16384 carbon atoms, the number of MPI processes is 19, and atoms with the same color are allocated to the same MPI process. It is found that a domain decomposition keeping locality is realized even using a prime number, 19, for the number of MPI processes.

We implemented the method in OpenMX [2], and performed a series of benchmark calculations for the O(N) Krylov subspace method on the K-computer. It was confirmed that the parallel efficiency is 68 % using 131072 cores on the K-computer for a diamond lattice consisting of 131072 carbon atoms, where the parallel efficiency was calculated by using the result by 16384 cores as a reference. With these efficient methods we have been investigating desolvation processes of Li ion at electrode-electrolyte interfaces appearing in Li-ion batteries and stability and electronic structures of metal-insulator interfaces in structural materials.
