
Research Highlights:
Massive parallelization of multi-dimensional FFTs with minimum communication amount
Fast Fourier Transforms (FFTs) play an important role in efficient implementations of first-principles electronic structure methods. Especially in the implementations based on plane-wave basis set FFT can be a bottleneck for the performance enhancement. Thus, it is important to develop an efficient FFT library. In recent years massively parallel computers consisting of a several thousand cores come to the forefront, thereby it would be desirable to develop a highly efficient parallelization method of multi-dimensional FFTs to extend applicability of applications using FFTs.
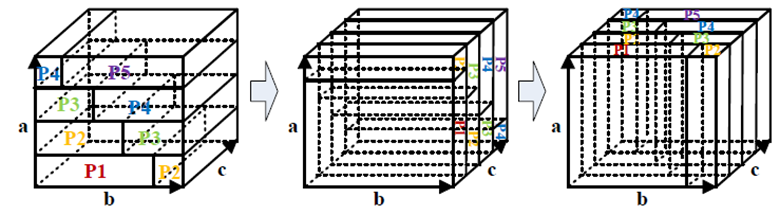
We have addressed development of a novel domain decomposition to reduce communication amount in the parallelization using message passing interface (MPI) on distributed memory computers [1], and found that the communication amount among MPI processes can be minimized by introducing a domain decomposition in a row-wise type as illustrated in Fig. 1. In the domain decomposition after mapping FFT grids in the multi-dimensional FFT in the row-wise type into an one-dimensional array, the FFT grids are assigned to each MPI process so that the computational cost can be well balanced. The mapping is not unique, and cases of (M-1)!M can be considered for M-dimensional FFT. We have investigated the communication amount of all the possible cases for 3-, 4-, and 5-dimensional FFTs in details, and indentified 4, 4, and 96 best cases, respecively, which have the lowest equivalent communication amount for any number of grids. Furthermore, we have compared our method with one-, 1.5-, 2-, and 3-dimensitonal domain decomposition methods proposed so far with respect to the communication amount, and found that our method has the minimum communication amount for any number of grids among them. The reduction of communication amount in our method is attributed to reusability of the data. In the multi-dimensional FFTs, a series of trasposition of the domain decomposion is performed after one-dimensional FFTs along an one-dimension in order to proceed the next dimension. The MPI communication is required in the trasposition, and one can reduce the communication amount by reusing the data without performing the MPI communication if the data stored in each MPI process has a large overlap before and after the trasposition. In fact, it turns out that our method has the largest overlap of data before and after the trasposition, minimizing the MPI communication amount.
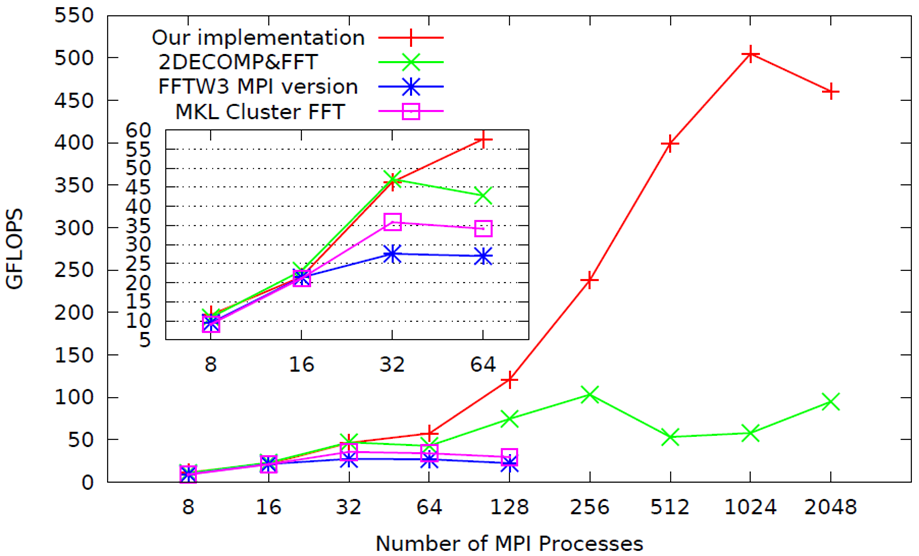
We have implemented the method, developed a library called OpenFFT, and made a pubic release of the library under GNU-GPL [2]. OpenFFT can be utilized from C and Fortran, and FFTW3 [3] is used for the one-dimensional FFT. On Cray-XC30 installed in JAIST, we have performed a series of benchmark calculations by estimating the GFLOP value based on the elapased time. Figure 2 shows a performace comparison of four FFT libraries (OpenFFT, 2DECOMP, parallel FFTW3, and MKL Cluster FFT) for 3D-FFT. We see that OpenFFT scales well up to a large number of MPI cores. With the good scalability of OpenFFT, we would expect that OpenFFT will be utilized for a wide variety of scientific simulations more than its application to first-principles electronic structure methods. On the other hand, we have also noticed that it is not easy to make the MPI communication localized in the mapping of the row-wise type, implying that the performance of our method will decrease in case of MPI parallelization using hundred thousand cores. The improvement of localization in the MPI communication will be a future study. It is also noted that the parallelization method has been employed in our DFT code: OpenMX [4].
