
Research Highlights:
A special Fermi-Dirac function accerelates convergerce
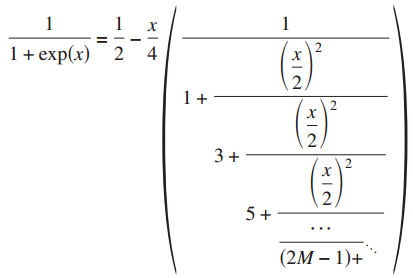
The Fermi-Dirac function is one of most important functions in condensed matter physics, and appears as integrand together with Green's functions in many electronic structure calculations regardless of ab initio or semi-empirical schemes. Such examples are the Korringa-Kohn-Rostoker (KKR) Green function method, Green's function based O(N) methods such as a recursion method, a surface Green's function method such as an embedded method, and Green's function methods based on a many body perturbation theory such as the GW method. Therefore, it is obvious that a highly accurate and efficient method must be developed for the integration to extend applicability of these electronic structure calculation methods. We tried to seek an efficient and accurate representation of the Fermi-Dirac function, and found that a continued fraction representation derived from a hypergeometric function is a proper expression for the purpose [1]. Numerical illustrations based on the density functional theories show that the method provides remarkable convergence with a small number of poles. The roots of the rapid convergence lies on an interesting non-uniform distribution of the poles on the imaginary axis for the representation of the Fermi-Dirac function, and it may be considered to be a generalization of the Matsubara poles with respect to distribution of poles so that the integration of the Green's function can converge rapidly. The finding enabled us to develop an efficient non-equilibrium Green's function (NEGF) method [2] and a numerically exact low-order scaling method for diagonalization [3]. It is also expected that the method can be applied to not only first principle electronic structure methods, but also a wide variety of model theories [4].
- "Continued fraction representation of the Fermi-Dirac function for large-scale electronic structure calculations", T. Ozaki, Phys. Rev. B 75, 035123 (2007).
- "Efficient implementation of the nonequilibrium Green function method for electronic transport calculations", T. Ozaki, K. Nishio, and H. Kino, Phys. Rev. B 81, 035116 (2010).
- "Efficient low-order scaling method for large-scale electronic structure calculations with localized basis functions", T. Ozaki, Phys. Rev. B 82, 075131 (2010).
- "Finite-temperature linear conductance from the Matsubara Green’s function without analytic continuation to the real axis", C. Karrasch, V. Meden, and K. Schonhammer, Phys. Rev. B 82, 125114 (2010).
