
Research Highlights:
フェルミ-ディラック関数の連分数表示
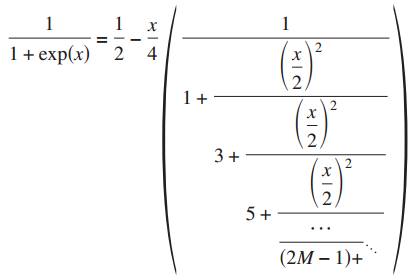
フェルミ-ディラック関数は固体物理において最も重要な関数の一つです。 この関数は第一原理手法か半経験的手法にかかわらず、多くの電子状態計算手法においてグリーン関数の積分で登場します。 例えばKorringa-Kohn-Rostoker(KKR)グリーン関数法、リカージョン法、表面グリーン関数法、 GW法などが、その例として挙げられます。これらの電子状態計算手法の適用限界を拡張するためには、グリーン関数の 積分を高精度かつ高速に実行することが重要です。
私達はこの積分の収束を加速させるため、フェルミ-ディラック関数に対する新しい表示形の探索を行いました。 そして超幾何関数から導出された連分数表示が、この積分の収束を著しく加速させることを見出しました[1]。 本手法により全エネルギーを計算した場合、高々80ポール程度で倍精度限界まで収束することが分かりました。 この高い収束性は連分数表示の持つ特殊なポール構造に起因しています。 連分数表示のポールは良く知られた松原ポールと同様に虚軸上に位置していますが、連分数を有限長で 打ち切った場合、隣接ポールの間隔が実軸を離れるに従い、急激に大きくなります。 グリーン関数は実軸上にポールを持っており、実軸を離れるとなだらかな関数で1/zに漸近します。 連分数表示の持つ特殊なポール構造は、この遠方でのグリーン関数の振舞いを効率的にサンプリング できるため、積分の収束が加速するのです。 私達はこの手法を非平衡グリーン関数法[2]と低次スケーリング対角化法[3]に応用しました。 また多体モデル計算に対しても本手法は成功裏に応用されています[4]。
