Research Highlights:

O(N) Krylov-subspace method for large-scale systems

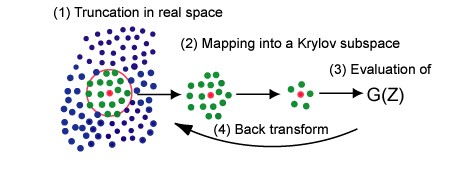
The computational cost of conventional density functional theories (DFT) calculations scales as the third power of the number of atoms, which means that the computational time becomes a thousand times longer than that for an original system when you try to calculate a ten times larger system. This presents an apparent difficulty to researchers who deal with realistic large-scale problems. On another front, it is known that chemical properties of functional groups in molecules are mostly determined by local atomic arrangement. The chemical intuition may enable us to develop an efficient method which determines the local electronic structure by making use of mainly short-range information. Along this line, we have developed an efficient and robust O(N) method by unifying two ideas of the divide-conquer and Krylov subspace methods, shown in the upper figure, whose computational cost scales only linearly as a function of the number of atoms [1].

The O(N) computational cost is guaranteed by the idea of the divide-conquer method, and the reduction of dimension by the Krylov subspace method provides a small computational prefactor. The practical algorithm is cast to solving a series of embedded cluster problems defined in Krylov subspaces. The O(N) method is expected to be a promising approach for realization of large-scale ab initio calculations for a wide variety of materials, since it is applicable to not only insulators but also metals in a single framework. 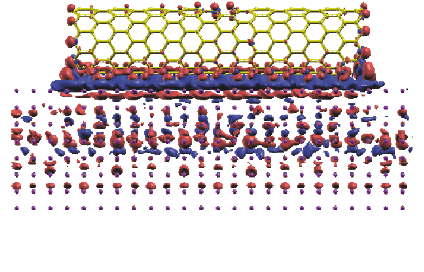The bottom figure shows difference charge density caused by the interaction between Al (001) and a (10,0) zigzag carbon nanotube, calculated by the O(N) method. We have been applying the O(N) method to various interface problems such as electrode-electrolyte and metal-insulator.

1. "O(N) Krylov-subspace method for large-scale ab initio electronic structure calculations", T. Ozaki, Phys. Rev. B 74, 245101 (2006).