
Research Highlights:
O(N)第一原理電子状態計算の超並列化手法
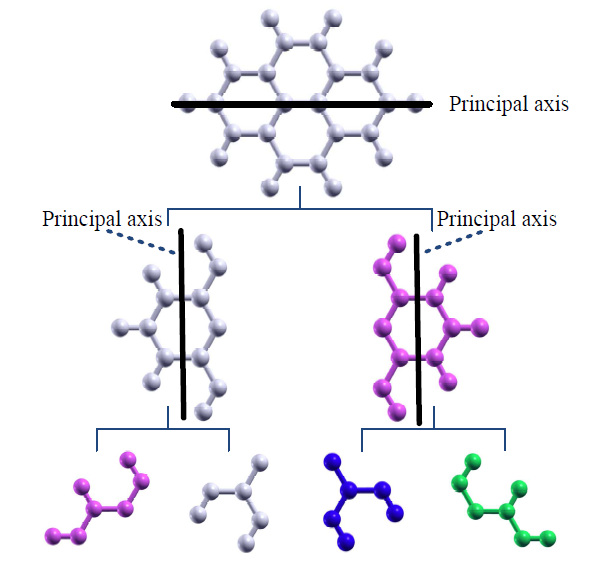
第一原理電子状態計算を大規模系へ拡張する方法の一つは、 計算量が原子数に比例するO(N)法を用いることです。 これまでに我々はO(N)クリロフ部分空間法の開発を行い、本手法が絶縁体だけでなく、 金属にも適用可能であることを実証してきました。 本手法は系を小さなクラスターに分割し、それぞれの計算を独立に行った後に、 中心原子のグリーン関数をパッチワークのように集約する手法で分割統治法の一つです。 そのアルゴリズムは本質的に並列計算に適しています。 しかし任意形状の系を任意のMPIプロセス数を用いて並列計算を行う場合、 いかにして系の分割を行えば、通信量と使用メモリを低減させることが出来るのか、 それほど自明ではありません。 並列化効率を向上させるためには、各プロセスの持つデータの局所性を高め、 プロセス間の通信量・回数を最小化することが重要です。 また計算負荷を均等化し、ロードバランスを保つ必要があります。 我々はこの要求を満足する領域分割法の開発に取り組み、 修正再帰二分法と慣性モーメントテンソルに基づく領域分割が適切な方法であることを見出しました [1]。
本手法は(1) 与えられたMPIプロセス数を修正再帰二分法を用いて二分木構造に分解するステップ、 (2) 原子群に対する慣性モーメントテンソルの対角化から主軸を決定し、その主軸上に原子を射影するステップ、 (3) ステップ(1)で計算した二分木を利用して主軸上で原子を分割するステップ、から構成されています。 図1に示すようにステップ(2)と(3)をステップ(1)で構築した二分木を用いて再帰的に行うことで、 局所性を保持した原子の空間分割が可能です。 また慣性モーメントテンソルを構築する際の重みとして構造最適化や分子動力学計算での1ステップ前の各原子の計算時間を用いることで、 動的にロードバランスを保つことも可能です。 一例として、本手法によって領域分割されたダイヤモンド格子を図1に示します。 ユニットセルには16,384個の炭素原子が含まれており、19個のMPIプロセスで分割した場合です。 同じ色の原子が同一のプロセスに割り当てられており、 素数である19分割でも空間局所性を保持した原子分割が実現されています。

我々は本手法をOpenMX [2] に実装し、O(N)クリロフ部分空間法の並列効率をスーパーコンピュータ「京」上で実測しました。 「京」の131,072コアを使用し、131,072原子から構成されるダイヤモンド格子に対して、 その並列効率は16,384コアを参照として68%であり、本手法の有効性が確認されました。 今後、本手法を活用して電極-電解質界面や金属-絶縁体界面などの大規模で複雑な系への適用研究を進めていきたいと考えています。
